2023年Q2用戶偏好榜：12+256G版本成新主流
3月份的性能榜、性價比榜和好評榜之后，就要輪到2023年的第二季度偏好榜了，上半年的新機潮已經(jīng)過去，最明顯的肯定就是大內(nèi)存和存儲的機型了，另外部分中端機也取消了屏幕塑料支架
知道自己寫的程序的時間復雜度，有利于我們寫出能夠高效運行的程序。
程序是由一個個函數(shù)組成的，有些簡單的由幾個基礎運算組成的函數(shù)大家一眼就能看出來它的時間復雜度，但是大部分函數(shù)沒那么簡單，只要函數(shù)里面涉及到了循環(huán)、外部函數(shù)調(diào)用甚至遞歸的時候它的時間復雜度就沒那么容易分析啦。
這篇文章的內(nèi)容，可以幫你快速推導出程序代碼的時間復雜度。
要分析程序的時間復雜度，首先還是要確定時間復雜度的度量標準— —英文文檔里通常會用 metric 這個單詞來表示，這個標準規(guī)定了在函數(shù)中平鋪展開的代碼、循環(huán)中的代碼、有函數(shù)調(diào)用的代碼、以及遞歸調(diào)用的代碼的時間復雜度的測量方式。
如何計算程序的時間復雜度呢？最常用的度量方式叫做 Big O Notations 翻譯過來叫大O標記法。
使用大O標記法前要先了解它的幾個要點：
在大O標記法中，常見的時間復雜度有一下幾類。
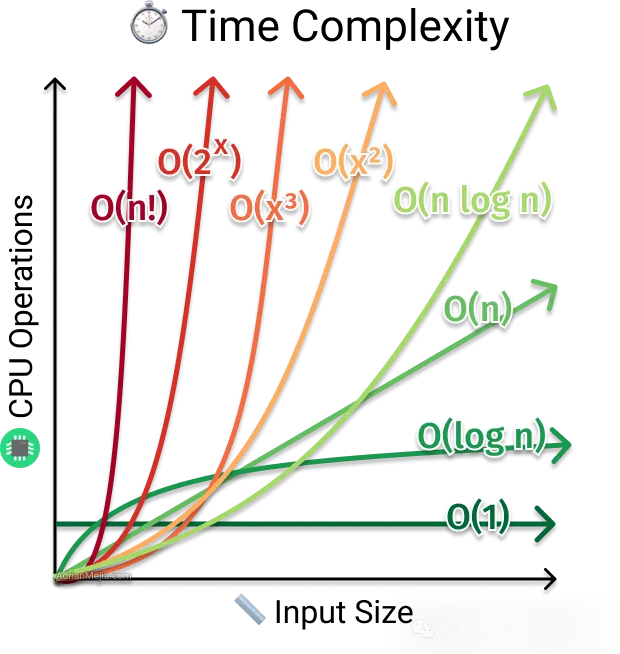
它們的關(guān)系如下：
圖片
從上面的圖我們可以看到，O(1)是最高效最穩(wěn)定的，完全不受輸入數(shù)據(jù)尺寸增長的影響，指數(shù)階隨著輸入的增加而爆增，而對數(shù)階則增長緩慢。
按照時間復雜度從低到高排序：
O(1) < O(logn) < O(n) < O(n log n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
在寫程序時，我們要注意時間復雜度增量的問題，盡量避免爆炸級增長。
了解完時間復雜度的大O標記法后，接下來我們看下怎么把我們平時接觸的代碼轉(zhuǎn)化為其對應的時間復雜度。
這是最簡單的代碼結(jié)構(gòu)，比如說我們有一個下面的計算3個數(shù)字的平方和的函數(shù)。
function squareSum(a, b, c) { const sa = a * a; const sb = b * b; const sc = c * c; const sum = sa + sb + sc; return sum;}函數(shù)中的每個語句都是一個基本運算。每行的時間復雜度為 O(1)。我們把所有語句的時間加起來，它仍然是 O(1)， 記住昂，不是O(3)。
O(1)表示程序時常數(shù)級的時間復雜度，不管程序的輸入是什么程序都會運行數(shù)量固定的操作。
注意如果順序排列的代碼中有對函數(shù)的調(diào)用，復雜度就不是O(1)了，你想知道是多少？
很少有會有程序代碼沒有任何條件語句。因為大 O 標記法關(guān)注程序運行的的最壞情況，所以對一個類似這樣的條件語句：
if (isValid) { statement1; statement2;} else { statement3;}它的時間復雜度可以按下面這個公式推導出來：
T(n) = Math.max([t(statement1) + t(statement2)], [time(statement3)])比如說下面這個代碼：
if (isValid) { array.sort(); return true;} else { return false;}if代碼塊中的時間復雜度為O( n log n) — 常用編程語言內(nèi)置排序算法的時間復雜度，else代碼塊的時間復雜度為O(1)，那么整個代碼的時間復雜度為：
O([n log n] + [n]) => O(n log n)for (let i = 0; i < array.length; i++) { statement1; statement2;}對于這個例子，循環(huán)執(zhí)行 array.length次，所有與輸入數(shù)據(jù)增長而成比例增長的循環(huán)都具有線性—常數(shù)階的時間復雜度 O(n)。
觀察下面的程序：
function fn(n) { i = 1; while( i < n) { i = i*2; } }對于這個程序，我們無法確定while 以及 i = i*2 語句運行了多少次，這時可以假設運行了x次，每次運行后i的值為2、22、23… 當while 語句的條件不滿足即i = n時結(jié)束，也就是2x = n ， x = log2n ，它的時間復雜度近似于O(logn )。
for (let i = 0; i < 4; i++) { statement1; statement2;}針對固定條件的循環(huán)，像上面這個程序一樣，無聊時固定循環(huán)4次還是 100 次時間復雜度都是 O(1)。
for (let i = 0; i < n; i++) { statement1; for (let j = 0; j < m; j++) { statement2; statement3; }}假設循環(huán)中的語句都是基礎操作，沒有對函數(shù)的調(diào)用，那么這個代碼有兩層嵌套循環(huán)，時間復雜度為O(n2)。
假如我們有這樣一個程序：
for (let i = 0; i < n; i++) { fn1(); for (let j = 0; j < n; j++) { fn2(); for (let k = 0; k < n; k++) { fn3(); } }}根據(jù) fn1、fn2 和 fn3 函數(shù)自身的時間復雜度，整個程序?qū)碛胁煌倪\行時間。
如果這三個函數(shù)它們都是常數(shù)階 O(1)，那么最終的運行時間將為 O(n3)。但是如果只有 fn1 和 fn2 是常數(shù)介， fn3 的時間復雜度為 O(n2)，則該程序的運行時間將為 O(n5)。
一般來說，循環(huán)中有函數(shù)調(diào)用，時間復雜度可以用下面這個公式計算：
T(n) = n * [ t(fn1()) + n * [ t(fn2()) + n * [ t(fn3()) ] ] ]function fn(n) { if (n == 1 || n == 2) { return 1; } return fn(n - 1) + fn(n - 2);}以上是學算法都學過的斐波那切數(shù)列的遞歸調(diào)用實現(xiàn)版本，它的時間復雜度為O(2n) ，所以在平時寫代碼時在你不確定程序能執(zhí)行多少次的時候，最好不要輕易使用遞歸調(diào)用。
這篇內(nèi)容我們梳理了一下不同的時間復雜對大概對應什么樣的代碼，讓我們能更正確地估算自己寫的程序的時間復雜度。
本文鏈接：http://www.www897cc.com/showinfo-26-89409-0.html怎么計算我們自己程序的時間復雜度
聲明：本網(wǎng)頁內(nèi)容旨在傳播知識，若有侵權(quán)等問題請及時與本網(wǎng)聯(lián)系，我們將在第一時間刪除處理。郵件：2376512515@qq.com
Copyright ? 2016-2023 天津谷騏科技有限公司 版權(quán)所有 sitemap.xml
違法及侵權(quán)請聯(lián)系：2376512515@qq.com 津ICP備18001702號
津公網(wǎng)安備 12010102000574號